Subband Processing

Speech signal processing is typically performed in the frequency domain for the sake of computational efficiency [HAY02]. Subband processing is an elegant way of transforming a block of speech signal between the time and subband frequency domains [HAY02] [VAD92]. The perfect reconstruction can be also achieved through the aliasing cancellation in subband processing. However, adaptive filtering systems would destroy perfect reconstruction property by scaling the magnitude of a subband and shifting the phase. Therefore, perfect reconstruction filter bank systems are not suitable for adaptive processing. We will instead need to reduce the aliasing distortion effect caused by arbitrary magnitude scaling and phase shifting [KMSK+08] [DGCN03]. This page explains how subband processing can be implemented with the BTK.

Oversampled DFT-modulated Filter

Subband processing with the oversampled DFT-modulated filter bank can be viewed as a more general form of traditional short-term FFT analysis method. A typical oversampled DFT-modulated filter bank will have the following parameters:

• Number of subbands, M, to control the frequency resolution
• Exponential decimation factor, r, to adjust the shift amount, and
• Filter length factor, m, to determine the length of the filter prototype.

Fig. 1 illustrates a block chart of the oversampled DFT-modulated filter bank. As shown in Fig. 1, the time-discrete signal is first transformed into the subband frequency domain through the analysis filter bank and decimator. After up-sampling, the subband component is then transformed back into the time domain through the synthesis filter bank. Analysis and synthesis filter bank processing can be done by using the OverSampledDFTAnalysisBankPtr and OverSampledDFTSynthesisBankPtr feature pointer objects respectively.

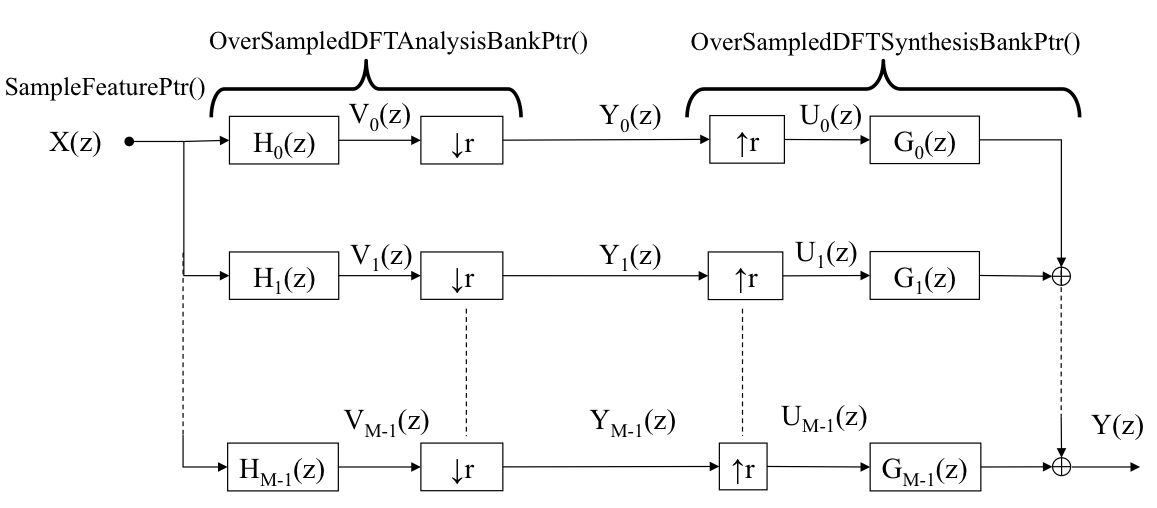
Fig. 1 Schematic view of subband processing with oversampled DFT-modulated filter bank

Nyquist(M) Filter Design

The Nyquist(M) filter is proven to lead to good performance in adaptive processing [KMSK+08]. We first need to generate analysis and synthesis filter coefficients by running tools/filterbank/design_nyquist_filter.py in the Git repository as follows.

$ cd ${your_btk_git_repository}/tools/filterbank
$ python design_nyquist_filter.py -M 128 -m 4 -r 1
nmin eigen val: (7.62745742563e-08+0j)
:152: ComplexWarning: Casting complex values to real discards the imaginary part
  h[m] = rh[k]
Inband aliasing error: -163.889262 dB
Use Lagrange multiplier...
Residual aliasing distortion: -122.681086 dB

Here, M, r and m are the number of subbands, exponential decimation factor and filter length factor, respectively.

By default, that command will dump files into a “prototype.ny” directory.

$ ls prototype.ny
M=128-m=4-r=1.m    g-M128-m4-r1.pickle         h-M128-m4-r1.pickle

With those files, we can test the Nyquist(M) filter bank system as follows.

$ python test_oversampled_dft_filter.py \
      -a prototype.ny/h-M128-m4-r1.pickle  \
      -s prototype.ny/g-M128-m4-r1.pickle  \
      -M 128 -m 4 -r 1 \
      -i Headset1.wav \
      -o wav/output.wav
Loading analysis prototype from 'prototype.ny/h-M128-m4-r1.pickle'
Loading synthesis prototype from 'prototype.ny/g-M128-m4-r1.pickle'
RMSE: 0.490225003654
Amplification ratio: 0.940362930298

The RMSE in the stdout indicates that the reconstruction error is negligible.

Listing 3 shows the inside of tools/filterbank/test_oversampled_dft_filter.py. The dependency of the feature pointer object is defined at line 45-49. The iterator of the synthesis filter bank system is called at line 62.

Listing 3 test_oversampled_dft_filter.py

#!/usr/bin/python
"""
Test the oversampled DFT-modulated filter bank such as de Haan and Nqyust(M) filter.

The filter prototypes have to be generated with design_de_haan_filter.py or design_nyquist_filter.py.

References:
[1] Jan Mark De Haan, Nedelko Grbic, Ingvar Claesson, Sven E Nordholm, "Filter bank design for subband adaptive microphone arrays", IEEE TSAP 2003.

[2] Kenichi Kumatani, John McDonough, Stefan Schacht, Dietrich Klakow, Philip N Garner, Weifeng Li, "Filter bank design based on minimization of individual aliasing terms for minimum mutual information subband adaptive beamforming", ICASSP 2018.

.. moduleauthor:: John McDonough, Kenichi Kumatani <k_kumatani@ieee.org>
"""
import os.path
import pickle
import wave
import sys
import numpy

from btk20.common import *
from btk20.stream import *
from btk20.feature import *
from btk20.modulated import *

def test_oversampled_dft_filter(analysis_filter_path,
                                synthesis_filter_path,
                                M, m, r,
                                audio_path,
                                out_path,
                                samplerate=16000):

    D = M / 2**r # frame shift

    # Read analysis prototype 'h'
    with open(analysis_filter_path, 'r') as fp:
        print('Loading analysis prototype from \'%s\'' %analysis_filter_path)
        h_fb = pickle.load(fp)

    # Read synthesis prototype 'g'
    with open(synthesis_filter_path, 'r') as fp:
        print('Loading synthesis prototype from \'%s\'' %synthesis_filter_path)
        g_fb = pickle.load(fp)

    # Instantiation of an audio file reader
    sample_feat = SampleFeaturePtr(block_len = D, shift_len = D, pad_zeros = True)
    # Instantiation of over-sampled DFT analysis filter bank
    afb = OverSampledDFTAnalysisBankPtr(sample_feat, prototype = h_fb, M = M, m = m, r = r, delay_compensation_type=2)
    # Instantiation of over-sampled DFT synthesis filter bank
    sfb = OverSampledDFTSynthesisBankPtr(afb, prototype = g_fb, M = M, m = m, r = r, delay_compensation_type=2)
    # Read the audio file
    sample_feat.read(audio_path, samplerate)

    if not os.path.exists(os.path.dirname(out_path)):
        os.makedirs(os.path.dirname(out_path))
    wavefile = wave.open(out_path, 'w')
    wavefile.setnchannels(1)
    wavefile.setsampwidth(2)
    wavefile.setframerate(int(samplerate))

    # Reconstruct the signal through the analysis and synthesis filter bank
    synthesized_signal = []
    for b in sfb:
        storewave = numpy.array(b, numpy.int16)
        wavefile.writeframes(storewave.tostring())
        synthesized_signal.extend(b)

    wavefile.close()

    # Obtain the original input signal
    sample_feat.read(audio_path, samplerate)
    original_signal = []
    for i in sample_feat:
        original_signal.extend(i)

    # Measure the root mean square error (RMSE)
    synthesized_signal = numpy.array(synthesized_signal)
    original_signal = numpy.array(original_signal)
    diff = synthesized_signal - original_signal
    rmse = numpy.sqrt(numpy.inner(diff, diff) / len(diff))
    print('RMSE: {}'.format(rmse))

    # Compute the ratio of synthesized signal strength to the original signal
    ratios = []
    for i in range(len(synthesized_signal)):
        if synthesized_signal[i] > 0:
            ratios.append( abs(original_signal[i] / synthesized_signal[i]) )
    print('Amplification ratio: {}'.format(numpy.average(numpy.array(ratios))))


def build_parser():
    import argparse

    M = 64
    m = 4
    r = 1

    # protoPath    = 'prototype.ny'
    # analysis_filter_path  = '%s/h-M%d-m%d-r%d.pickle' %(protoPath, M, m, r)
    # synthesis_filter_path = '%s/g-M%d-m%d-r%d.pickle' %(protoPath, M, m, r)

    v = 100.0
    wpW = 1
    protoPath    = 'prototype.dh'
    analysis_filter_path  = '%s/h-M=%d-m=%d-r=%d-v=%0.4f-w=%0.2f.pickle' %(protoPath, M, m, r, v, wpW)
    synthesis_filter_path = '%s/g-M=%d-m=%d-r=%d-v=%0.4f-w=%0.2f.pickle' %(protoPath, M, m, r, v, wpW)
    out_path = './wav/M=%d-m=%d-r=%d_oversampled.wav' %(M, m, r)

    parser = argparse.ArgumentParser(description='run subband processing with oversampled DFT-modulated filter bank.')
    parser.add_argument('-a', dest='analysis_filter_path',
                        default=analysis_filter_path,
                        help='analysis filter prototype file')
    parser.add_argument('-s', dest='synthesis_filter_path',
                        default=synthesis_filter_path,
                        help='synthesis filter prototype file')
    parser.add_argument('-M', dest='M',
                        default=M, type=int,
                        help='no. of subbands')
    parser.add_argument('-m', dest='m',
                        default=m, type=int,
                        help='Prototype filter length factor')
    parser.add_argument('-r', dest='r',
                        default=r, type=int,
                        help='Decimation factor')
    parser.add_argument('-i', dest='audio_path',
                        default='Headset1.wav',
                        help='input audio file')
    parser.add_argument('-o', dest='out_path',
                        default=out_path,
                        help='output audio file')

    return parser


if __name__ == '__main__':

    parser = build_parser()
    args = parser.parse_args()

    test_oversampled_dft_filter(args.analysis_filter_path,
                                args.synthesis_filter_path,
                                args.M, args.m, args.r,
                                args.audio_path,
                                args.out_path,
                                samplerate=16000)

de Haan Filter Design

The BTK provides another oversampled DFT-modulated filter technique proposed by Jan Mark de Haan [DGCN03]. Although de Haan’s method has a higher reconstruction error than the Nyquist(M) filter bank, it may be interesting to try it.

The de Haan’s filter prototypes can be generated as:

$ cd ${your_btk_git_repository}/tools/filterbank
$ python design_de_haan_filter.py -M 128 -m 4 -r 1 -w 1.0 -v 100.0
M=128 m=4 r=1 D=64 v=100.000000 wp=pi/1*M
Calculating 'A' and 'b' ... Done
Calculating 'C' ... Done
Solving for analysis prototype 'h' ... Done.
eps_p = -59.764779
eps_i = -51.875200
Initializing 'SynthesisOversampledDFTDesign'.
Calculating 'E', 'P', and 'f' ... Done.
Solving for synthesis prototype 'g' ... Done.
eps_t = 2.948278
eps_r = -38.535916

You can test the de Haan’s filter in the same way as the Nyquist(M) filter as

$ python test_oversampled_dft_filter.py \
       -a prototype.dh/h-M=128-m=4-r=1-v=100.0000-w=1.00.pickle \
       -s prototype.dh/g-M=128-m=4-r=1-v=100.0000-w=1.00.pickle \
       -M 128 -m 4 -r 1 \
       -i Headset1.wav  \
      -o wav/output.wav
Loading analysis prototype from 'prototype.dh/h-M=128-m=4-r=1-v=100.0000-w=1.00.pickle'
Loading synthesis prototype from 'prototype.dh/g-M=128-m=4-r=1-v=100.0000-w=1.00.pickle'
RMSE: 7.48633662867
Amplification ratio: 1.006513834

Cosine-modulated Perfect Reconstruction Filter

Overlap-Add/Save Method